Олександр Рудик
Система Лоренца
як приклад динамічної системи
зі складною поведінкою
1. Причини інтересу до системи Лоренца
У даній публікації розглянуто складну поведінку динамічної системи на прикладі потоку, тобто зсуву за часом t вздовж траекторій — розв'язків системи звичайних диференціальних рівнянь:
| dx1/dt = – σx1 + σx2; | (1) |
| dx2/dt = – x1x3 + rx1 – x2; | (2) |
| dx3/dt = x1x2 – bx3. | (3) |
Тут σ, b та r — деякі додатні параметри.
Cистему (1–3) запровадив Е.Лоренц у ході моделювання конвектиного потоку рідини, що підігрівають знизу (Edward Norton Lorenz. Deterministic Nonperiodic Flow // Journal of the Atmospheric Sciences, 1963, volume 20, issue 2 (March), pp. 130–141). Такий потік описують за допомогою системи диференціальних рівнянь у часткових похідних. Систему Лоренца (1–3) отримують за допомогою певного наближення — проектування на деякий тривимірний підпростір нескінченовимірного простору функцій. Інакше кажучи, використанням методу Бубнова (1913) — Гальоркіна (Галёркин Б. Г. Стержни и пластинки. Ряды в некоторых вопросах упругого равновесия стержней и пластинок. // Вестник инженеров. — 1915. — Т. 1. — С. 897—908).
Ця публікація містить лише ті дані, які вже були опубліковані раніше. Програму мовою Reduce подано лише як зразок для дослідження стійкості особливох точок. Для системи Лоренца використання такої програми не є необхідним.
У ході чисельного інтегрування системи (1–3) Е.Лоренц виявив, що при σ = 10, b = 8/3, r = 28 траекторії цієї динамічної системи одночасно демонструють хаотичну нерегулярну поведінку і притягуються до певної множини зі складною структурою, яку називають атрактором (від. англ. to attract — притягувати). На рис. 1–3 подано залежність від часу t∈[0; 20] розв'язків системи рівнянь при таких початкових значень:
x1 = 1.26409225509719;
x2 = 3.20967915187994;
x3 = 21.7503050834145
при вказаних значеннях параметрів сисеми Лоренца. Ці розв'язки отримано чисельним інтегруванням системи Лоренца при тих самих значеннях параметрів на проміжку [0; 106] і таких початкових значеннях: x1 = x2 = x3 = 1.
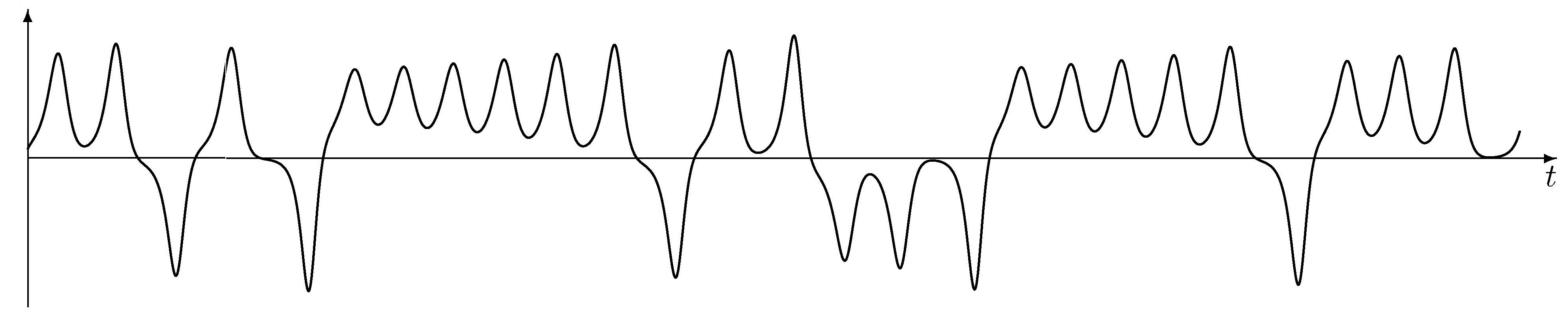
Рис. 1. Залежність x1 розв'язку системи Лоренца від часу t∈[0; 20].
Зображено відрізок [–20; 20] осі x1.
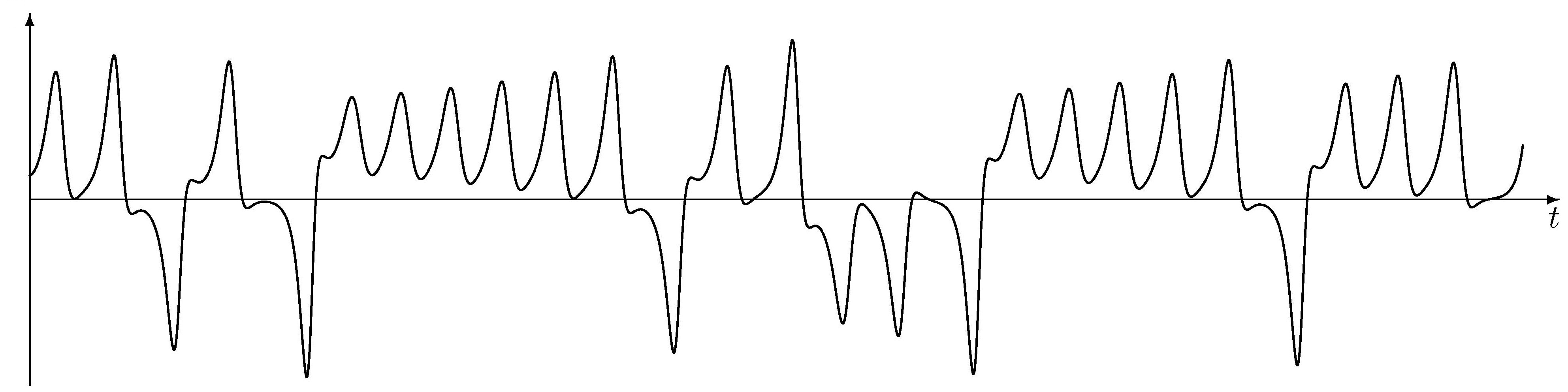
Рис. 2. Залежність x2 розв'язку системи Лоренца від часу t∈[0; 20].
Зображено відрізок [–25; 25] осі x2.
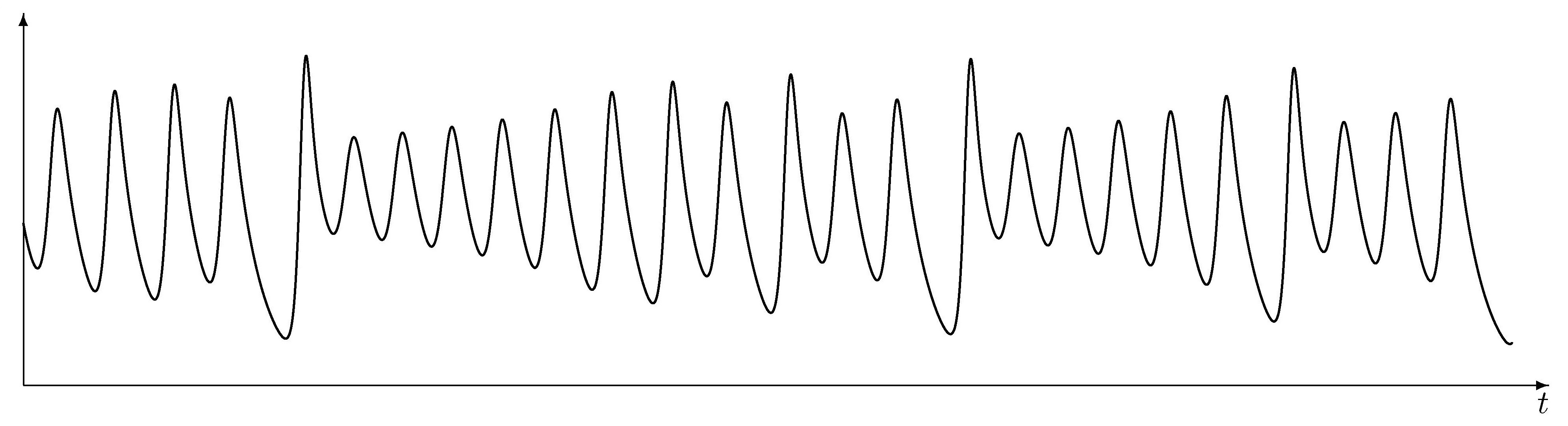
Рис. 3. Залежність x3 розв'язку системи Лоренца від часу t∈[0; 20].
Зображено відрізок [0;50] осі x3.
Такою поведінку траекторій природно пов’язали з турбулентним потоком рідини. Але остаточно невідомо, чи турбулентність пов'язана з хаотичністю руху у скінченовимірному просторі коефіцієнтів проекції, чи саме з нескінченовимірністю простору функцій, що описують потік рідини.
Зазвичай пересічні люди далекі від проблем опису турбулентності. Але прогнозами погоди цікавляться усі, у тому числі, з економічних міркувань. Система Лоренца виникла саме у процесі математичного моделювання метеорологічних процесів з метою створення точних синоптичних прогнозів. Сучасні моделі метеорологічних процесів ґрунтуються на нелінійних диференціальних рівняннях у часткових похідних. Можливо, непередбачуваність погоди пояснюється наявністю складної структури відповідного атрактора, а не лише випадковими втручанням космічних сил.
Питання має значну передісторію. Ще у 1814 році французький вчений П’єр-Симон Лаплас запровадив поняття демона, що був предметом наукових дискусій протягом тривалого часу. Видуманий демон знав розташування і швидкості кожної частинки у Всесвіті і, знаючи усі фізичні закони, міг передбачити мабутнє кожної частинки й описати її минуле. Чи можливий такий демон теоретично? Успіхи науки Нового часу (розрахунок орбіт планет, передбачення появи комет) давали надію на ствердну відповідь.
У 1927 році німецький фізик Вернер Гайзенберг відкрив принцип невизначенності. Пояснимо принцип на прикладі пари декартова координата + проекція імпульса на відповідний напрям. Розглянемо ансамбль (сукупність) еквівалентних частинок, що не взаємодіють між собою і знаходяться в одному стані. При вимірюванні координати x та імпульса p результати вимірювання будуть випадковими, а їхні дисперсії (середньо квадратичні відхилення від середніх значень) Δx та Δp задовольняють таку нерівність:
Δx · Δp ≥ ћ /2.
Тут ћ = 1,054 571 628(53) · 10–34 Дж·с — стала Дірака — зведена стала Планка. У загальному випадку принцип невизначеності виникає між довільними змінними, яким відповідають оператори квантової механіки, що не комутують — для яких результат послідовного застосування залежить від порядку застосування. Таким чином, квантові системи принципово непідвладні демону Лапласа.
Згодом зауважили, що існування демона суперечило б законам термодинамики: йому не вистачило б знань та інформаційних ресурсів Всесвіту для вичерпного передбачення його майбутнього. Але чи є принципові труднощі для демона Лапласа (читай суперкоп’ютера) у випадку ізольованої скінченої повністю детермінованої системи?
Довільні фізичні вимірювання містять певну помилку. Змінні у пам’яті комп'ютера зберігаються з певною точністю.
Можливо достатньо обмежитися кількома значащими цифрами у початкових данних, щоб бути впевненим у кінцевому результаті хоча б з певною точністю?
Система Лоренца — це хронологічно перший приклад системи звичайних диференціальних рівнянь, розв’язки якої істотно чутливі до початкових значень. Настільки чутливі, що породили поняття «детермінований хаос», яке традиційно вживають для позначення нерегулярної та непередбачуваної поведінки детермінованих нелінійних динамічних систем. Чи округлення у теоретичній моделі, чи похибка вимірювання у реальній системі — і система веде себе кардинально по іншому.
Лоренц міркував так: якщо погода справді належить до настільки чутливих систем, то помах крил чайки може викликати істотні зміни погоди. Згодом чайку замінили на метелика, а в 1972 році з’явилася работа «Передбачуваність: чи може помах крил метелика в Бразилії призвести до торнадо в Техасі?». Так народився знаменитий термін «ефект метелика», що викликає асоціації з науково-фантастичним оповіданням Рея Бредбері та з відкриттям Лоренца – дивним атрактором, названим на його честь.
2. Результати часткового дослідження системи Лоренца
Стаціонарні (нерухомі) точки системи Лоренца можна знайти, прирівнявши до нуля праві частини рівнянь (1–3):
-
з рівності dx1/dt = 0 маємо: x1 = x2 ;
-
з рівності dx2/dt = 0 та першого висновку маємо: x1( – x3 + r – 1) = 0;
-
з рівності dx3/dt = 0 та першого висновку маємо: (x1)2 = bx3.
Матриця ∂f(x)/∂x (похідна подя напрямів) для системи Лоренца має такий вигляд.
| – σ | σ | 0 |
| r – x3 | – 1 | – x1 |
| x2 | x1 | – b |
Власні числа λ матриці ∂f(x)/∂x задовольняють характеристичне рівняння:
\[ {\rm det}\left(λ – {∂f\over ∂x}(x)\right) = 0.\]
Тут det (A) — визначник матриці A.
Подамо сценарій зміни поведінки системи Лоренца (1–3) при сталих σ = 10, b = 8/3 і зростанні r від нуля.
Аналітичні дослідження стійкості нерухомих точок можна проводити і традиційно «на кінчику пера», і за допомогою спеціального програмного забезпечення. Скористаємося нагодою, щоб показати використання системи алгебричних обчислень Reduce, запозиченої з ресурсу http://reduce-algebra.sourceforge.net/. Код програми має такий вигляд (знак % позначає початок коментаря, кінець якого є кінцем відповідного рядка).
off nat, % Виведення в один рядок
echo; % Блокування виведення ракції на команди
order z; % Запис характеристичного рівняння
% відносно власного числа z
% у порядку спадання степенів z
factor z; % Групування одночленів з однаковим
% степенем z
n:=3; % Розмірність фазового простору -
% кількість динамічних змінних
% Виділення назв для:
array x(n), % динамічних змінних х,
f(n), % поля напрямків f,
l(n); % власних чисел fx
matrix fx(n,n); % матриці похідних f за x
% Задання вектор-стовпчика динамічних змінних
x(1):=x1;
x(2):=x2;
x(3):=x3;
% Задання поля напрямків f
f(1):=s*(x2-x1);
f(2):=-x1*x3+r*x1-x2;
f(3):= x1*x2-b*x3;
% Визначення значень параметрів
s:=10;
b:=8/3;
% Знаходження похідної поля напрямків
for j:=1:n do
for k:=1:n do fx(j,k):=df(f(j),x(k));
for j:=1:n do fx(j,j):=fx(j,j)-z;
% Знаходження списку стаціонарних точок x0
x0:=solve(
{f(1),f(2),f(3)}, % Ліві частини рівнянь за умови,
% що праві частини дорівнюють 0
{x1,x2,x3}); % невідомі змінні
n0:=length(x0); % Кількість стаціонарних точок
% (у тому числі уявних)
out "result.txt"; % Визначення файлу виведення
for j:=1:n0 do <<
write("______________________________________");
write("Координати стаціонарної точки № ",j,":");
for k:=1:n do <<
y:=part(x0,j,k);
write(y);
let y >>;
write("Похідна поля напрямків:");
let z=0;
for k:=1:n do for l:=1:n do
write("df",k," / dx",l," = ",fx(k,l));
clear z;
polynom:=det(fx);
write("Характеристичне рівняння: ",
(-1)**n*polynom," = 0");
z0:=solve(polynom=0,z); % Cписок власних чисел
if length(z0)>1 then <<
write("Власні значення - корені ",
"характеристичного рівняння:");
for k:=1:n do write(part(z0,k)) >>;
clear x1,x2,x3 % Вивільнення змiних;
>>;
shut "result.txt";% Закриття файлу виведення
end;
Після виконання цієї програми файл result.txt матиме такий вигдяд (вилучено порожні рядки).
______________________________________
Координати стаціонарної точки № 1:
x1=(2*sqrt(r - 1)*sqrt(2))/sqrt(3)
x2=(2*sqrt(r - 1)*sqrt(2))/sqrt(3)
x3=r - 1
Похідна поля напрямків:
df1 / dx1 = -10
df1 / dx2 = 10
df1 / dx3 = 0
df2 / dx1 = 1
df2 / dx2 = -1
df2 / dx3 = ( - 2*sqrt(r - 1)*sqrt(2))/sqrt(3)
df3 / dx1 = (2*sqrt(r - 1)*sqrt(2))/sqrt(3)
df3 / dx2 = (2*sqrt(r - 1)*sqrt(2))/sqrt(3)
df3 / dx3 = ( - 8)/3
Характеристичне рівняння: (3*z**3 + 41*z**2 + 8*z*(r + 10) + 160*(r - 1))/3 = 0
______________________________________
Координати стаціонарної точки № 2:
x1=( - 2*sqrt(r - 1)*sqrt(2))/sqrt(3)
x2=( - 2*sqrt(r - 1)*sqrt(2))/sqrt(3)
x3=r - 1
Похідна поля напрямків:
df1 / dx1 = -10
df1 / dx2 = 10
df1 / dx3 = 0
df2 / dx1 = 1
df2 / dx2 = -1
df2 / dx3 = (2*sqrt(r - 1)*sqrt(2))/sqrt(3)
df3 / dx1 = ( - 2*sqrt(r - 1)*sqrt(2))/sqrt(3)
df3 / dx2 = ( - 2*sqrt(r - 1)*sqrt(2))/sqrt(3)
df3 / dx3 = ( - 8)/3
Характеристичне рівняння: (3*z**3 + 41*z**2 + 8*z*(r + 10) + 160*(r - 1))/3 = 0
______________________________________
Координати стаціонарної точки № 3:
x1=0
x2=0
x3=0
Похідна поля напрямків:
df1 / dx1 = -10
df1 / dx2 = 10
df1 / dx3 = 0
df2 / dx1 = r
df2 / dx2 = -1
df2 / dx3 = 0
df3 / dx1 = 0
df3 / dx2 = 0
df3 / dx3 = ( - 8)/3
Характеристичне рівняння: (3*z**3 + 41*z**2 + 2*z*( - 15*r + 59) + 80*( - r + 1))/3 = 0
Власні значення - корені характеристичного рівняння:
z=(sqrt(40*r + 81) - 11)/2
z=( - sqrt(40*r + 81) - 11)/2
z=( - 8)/3
При r < 1 система Лоренца (1) має єдину стаціонарну (нерухому) точку — початок координат, до якого притягуються всі траекторії (рис. 4).
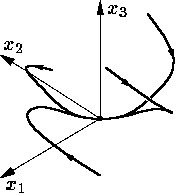
Рис. 4.
При r > 1 початок координат вже нестійкий, бо матриця ∂f/∂x має одне додатне і два від’ємних власних числа. Крім початку координат при r > 1 існує ще дві стаціонарні точки:
\[X_1 = \left( \sqrt{b(r – 1)}; \sqrt{b(r – 1)}; r – 1\right);\]
\[X_2 = \left( -\sqrt{b(r – 1)}; -\sqrt{b(r – 1)}; r – 1\right).\]
Спочатку всі власні числа λ матриці ∂f/∂ x у двох нових стаціонарних точках від’ємні (рис. 5).
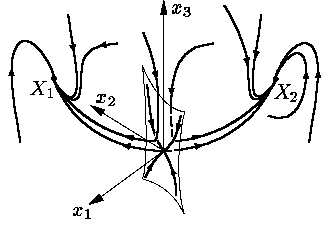
Рис. 5.
Згодом при зростанні r пара від’ємних власних чисел перетворюється на пару комплексно спряжених чисел з від’ємною дійсною частиною. Кожна з двох траекторії G1 і G2, що «виходять» з початку координат у напрямках власного вектора матриці ∂f(0)/∂x з додатним власним числом, і «входили» у стійку стаціонарну точку X1 чи X2, починають закручуватися спіраллю навколо цієї стаціонарної точки (рис. 6).
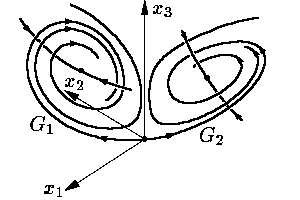
Рис. 6.
При r ≈ 13,92 траекторії Г1 і Г2 «входять» у початок координат у напрямку власного вектора матриці ∂f(0)/∂x з від’ємним власним числом (рис. 7).
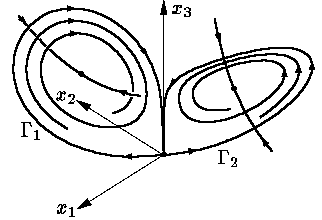
Рис. 7.
При подальшому зростанні r в околі ще стійких стаціонарних точок з’являються два нестійкі цикли Ф1 і Ф2. Лінійні частини операторів слідування для цих циклів мають по два власних значення, що лежать по різні боки від 1. Інакше кажучи, по одному напряму тракторії притягуються до цих циклів, а по іншому — відштовхуються. При цьому дві траекторії G1 і G2 притягуються вже до інших стаціонарних точок, ніж до появи нестійких циклів, і закручуються спіраллю навколо них (рис. 8).
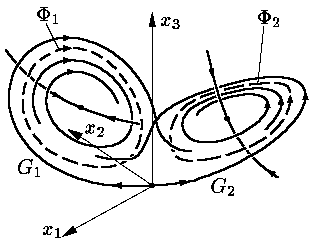
Рис. 8.
При r ≈ 24,06 траекторії G1 і G2 потрапляють на многовиди притягування до нестійких циклів Ф1 і Ф2.
При r = r0 = σ(σ + b + 3)/(σ – b – 1) ≈ 24,74 матриця ∂f(Xj)/∂x (j = 1, 2) має два комплексно спряжених власних числа на уявній осі. Дійсні частини цих власних чисел зростають при зростанні r. Стаціонарні точки X1 та X2 гублять свою стійкість, поглинаючи нестійкі цикли (так звана біфуркація Пуанкаре — Андронова — Хопфа).
Вже при r > 13.92 система Лоренца має граничну інваріантну множину, яка при r < r0 не є стійкою, тобто не притягує траекторії. При r ∈ (r0; 50]
ця множина стає стійкою. Її називають атрактором Лоренца. На рис. 9 подано двовимірну проекцію траекторії в околі атрактора Лоренца. Траекторія робить кілька обертів навколо однієї стаціонарної точки, потім — навколо іншої і т.і. Кількість таких послідовних обертів навколо стаціонарної точки настільки істотно залежить від координат початкової точки, що виникає враження хаотичності руху і, навіть, випадковості такого руху.
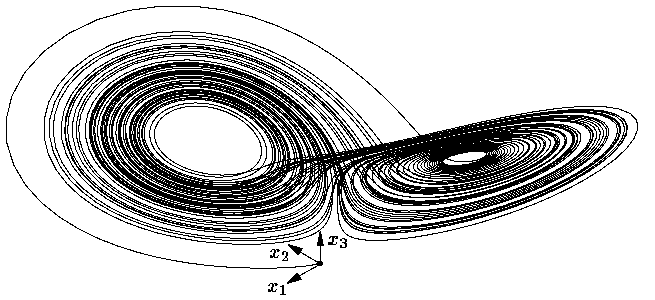
Рис. 9.
Для дослідження спостережуваної хаотичної поведінки Лоренц використав такий прийом:
-
занумерував локальні максимуми у хронологічному порядку (проходження в часі) і отримав деяку послідовність {\(z_j\)};
-
зобразив на координатній площині точки \((z_j;~z_{j+ 1})\), тобто унаочнив залежність величини поточного максимуму від попереднього.
Зовсім не очевидно, що такі дії можуть призвести до якогось розумного результату. Наприклад, до підтвердження існування деякого відображення g, при якому \(z_{j+1}=g(z_j)\). Виявляється, що точки \((z_j;~z_{j+ 1})\) таки належать певній кривій з гострою вершиною — див. рис. 10, запозичений зі згаданої вище оригінальної роботи Лоренца.

Рис. 10.
Таким чином, в околі атрактора дослідження динаміки розв'язків рівнянь Лоренца можна замінити аналізом динаміки одновимірного відображення \(z_{j+1}=g(z_j)\).
Необхідна умова екстремуму змінної — рівність нулю її похідної. Це у свою чергу визначає у просторі деяку поверхню. У даному випадку — гіперболічний параболоїд. На цій поверхні є область, в якій справджується достатня умова наявності максимуму \(z'' < 0\). Потік фазових траєкторій системи Лоренца задає на цій частині поверхні так зване відображення Пуанкаре: випустивши траєкторію з довільної точки B цієї області, дочекатися її наступного перетину у точці цієї області {\(z'' < 0\)}, що й буде образом точки B. Таке відображення Пуанкаре для системи Лоренца 2-вимірне. Але модель Лоренца характеризується дуже високим ступенем стискання елемента фазового об'єму за час між послідовними перетинами. Тому таке відображення Пуанкаре справді добре наближається одновимірним, що спостерігаємо на рис. 10. Хоча лише детальне дослідження відображення Пуанкаре дає можливість упевнено стверджувати щось про структуру атрактора.
Атрактор Лоренца A має такі властивості.
A є атрактором у тому розумінні, що існує відкрита в R3 множина B, при якій
Тут Tt — оператор зсуву вздовж траекторій системи на час t. Інакше кажучи, всі траекторії, що мають початок у B (для системи Лоренца за B можна взяти все R3 без стаціонарних точок), притягуються до A.
A містить всюди щільну множину періодичних траекторій, кожна з яких є нестійкою.
Для довільної траекторії в A з трьох різних характиристичних показників Ляпунова один дорівнює 0 (для напряму потоку f ), один — від’ємний (вздовж відповідного напряму відбувається притягування траекторій), а ще один — додатний (вздовж відповідного напряму відбувається експотенціальне «розбігання» траекторій навіть при як завгодно малих відхиленнях початкових значень).
Локально атрактор Лоренца має структуру добутку інтервалу на канторову множину.
При більших значеннях r виявлено стійкі періодичні розв'язки. Наприклад, при r = 234 система Лоренца має стійкий цикл. При зменшенні значення r такий цикл втрачає стійкість, породжуючи стійкий цикл подвоєного періоду. При подальшому зменшенні значення r новостворений цикл втрачає стійкість, породжуючи новий стійкий цикл подвоєного періоду і т.д. і т.і. Таким чином виникає нескінчена спадна послідовність {rk} значень параметра, при яких система Лоренца подвоює період стійкого циклу. Виявляється, ця послідовність задовольняє закону універсальності Фейгенбаума, тобто рівності:
lim
k → ∞
|
| rk – rk – 1
rk + 1 – rk
|
= δ, |
|
Тут δ = 4.6692… — певна універсальна стала, для якої доведено відповідне твердження для неперервних перетворень прямої (інтервала) в себе (Вул Е. Б., Синай Я. Г., Ханин К. М., Универсальность Фейгенбаума и термодинамический формализм // УМН, 1984, 39:3 (237), с. 3–37).
3. Існування обмеженої замкненої області, з якої не виходять траєкторії системи Лоренца
Доведемо, що у просторі можна вказати таку обмежену замкнуту область, у яку траєкторії системи Лоренца можуть лише входити і її не покидають. Для спрощення сприйняття записів використаємо таку форму запису рівнянь:\[\cases{
x'=-\sigma x+\sigma y,\cr
y'=-xz+rx-y,\cr
z'=xy-bz.}\]
Розглянемо функцію \[v(x,y,z) = rx^2 + \sigma y^2 + \sigma (z - 2r)^2,\] що набуває невід'ємних значень. Маємо:
\[{d\over dt} v(x,y,z) = 2rx\cdot x' + 2\sigma y\cdot y' + 2\sigma (z - 2r) \cdot z'\]
\[=2rx\cdot \sigma (y-x) + 2\sigma y\cdot (-xz+rx-y) + 2\sigma (z - 2r) \cdot (xy-bz)\]
\[=-2\sigma (rx^2 + y^2 + bz^2 − 2brz).\]
Визначимо область \[ \Omega =\{(x,y,z)\in R^3~|~rx^2 + y^2 + bz^2 − 2brz < 0\},\]
обмежену еліпсоїдом \[\partial\Omega =\{(x,y,z)\in R^3~|~rx^2 + y^2 + b(z − r)^2 = br^2\}\]
— сферою, стиснутою чи розтягнутою у двох перпендикулярних напрямках.
Для розв'язків системи Лоренца в області \(\Omega\) маємо: \[{d\over dt} v(x,y,z) > 0.\]
Виберемо додатне \(\varepsilon\) таким чином, щоб область \(\Omega\) разом зі своєю межею \(\partial\Omega\) була розташована всередині поверхні:
\[S_\varepsilon =\{(x,y,z)\in R^3~|~ rx^2 + \sigma y^2 + \sigma (z - 2r)^2=\varepsilon\}.\]
Якщо точка \((x_0,y_0,z_0)\) розташована зовні \(S_\varepsilon\), то вона також розташована поза \(\Omega\). Тоді для розв'язку системи Лоренца з початковими значеннями \((x_0,y_0,z_0)\) величина \(v(x,y,z)\) зменшується щонайменше до перетину з \(S_\varepsilon\) через скінчений проміжок часу. При цьому на самій поверхні \(S_\varepsilon\) маємо: \[ v(x,y,z)=\varepsilon ;\qquad {d\over dt} v(x,y,z) < 0.\]
Тому щойно траєкторія перетинає \(S\), вона вже не може вийти назовні \(S\).









