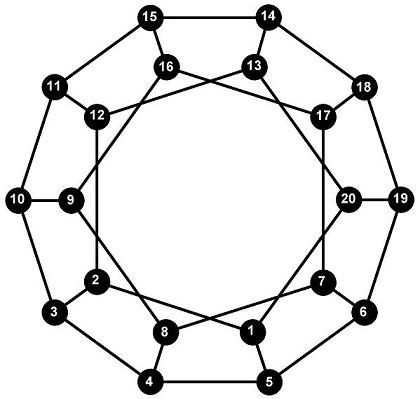
Рис. 1. Вершини правильного 12-гранника занумеровано
у порядку обходу гамільтоновим циклом.
Означення 1. Запровадимо такі поняття.
Ланцюгом (неорієнтованого) графа називають маршрут, всі ребра якого різні.
Ланцюг називають простим, якщо він не містить однакових вершин, можливо, за виключенням першої і останньої, якщо ланцюг замкнений.
Замкнений ланцюг називають циклом (або контуром).
Замкнений простий ланцюг називають простим циклом.
Гамільтоновим ланцюгом графа називають його простий ланцюг, що проходить через кожну вершину графа саме один раз.
Гамільтоновим циклом графа називають його простий цикл, що проходить через кожну вершину графа.
Граф називають гамільтоновим, якщо він має гамільтоновий цикл.
Запровадження цих понять пов'язане з іменем ірландського математика Гамільтона (William Rowan Hamilton, Account of the Icosian Calculus // Proceedings of the Royal Irish Academy, 1858, 6), який запропонував таку гру ломиголовку.
Задача 1. Рухаючись ребрами правильного 12-гранника, обійти всі його 20 вершин по одному разу й повернутися у початкову вершину.

Широко відомі ще й такі задачі 2–3.
Задача 2 (про шахового коня). Чи можна шаховим конем обійти всі 64 клітини шахової дошки й повернутися у вихідну точку?
| 30 | 3 | 22 | 9 | 28 | 5 | 24 | 15 |
| 21 | 10 | 29 | 4 | 23 | 16 | 27 | 6 |
| 2 | 31 | 12 | 19 | 8 | 25 | 14 | 17 |
| 11 | 20 | 1 | 32 | 13 | 18 | 7 | 26 |
| 58 | 39 | 50 | 45 | 64 | 33 | 52 | 43 |
| 49 | 46 | 57 | 40 | 51 | 44 | 63 | 34 |
| 38 | 59 | 48 | 55 | 36 | 61 | 42 | 53 |
| 47 | 56 | 37 | 60 | 41 | 54 | 35 | 62 |
Задача 3 (про бенкет). Розсадити за круглим столом компанію з кількох чоловік таким чином, щоб кожний з них сидів між своїми знайомими.
Розв'язок останньої задачі задає гамільтонів цикл на графі знайомств компанії.
Теорема 1 (достатні умови гамільтоновості графа).
Нехай граф G(V, E) має p вершин, 3 ≤ p = | V |. Якщо справджуються такі дві умови:
при довільному натуральному j, що задовольняє нерівності: 1 ≤ j < (p – 1)/2, кількість вершин, степінь яких не перевищує j, менша за j —
при непарному p кількість вершин, степінь яких не перевищує (p – 1)/2, не перевищує (p – 1)/2
то G — гамільтонів граф.
Доведення (від супротивного).
Нехай G — максимальний негамільтонів граф, що задовольняє умови теореми. Інакше кажучи, долучення довільного ребра, що сполучає наявні вершини графа, призводить до появи гамільтонового циклу.
Довільні дві несуміжні вершини v1 і vp графа G можна сполучити гамільтоновим ланцюгом:
Вершина vp не суміжна з будь-якою вершиною vk, при якій vk + 1 суміжна з v1, бо інакше можна отримати суперечність з негамільтоновістю графа G, побудувавши такий гамільтонів цикл:
Довільну вершину графа не вважають суміжною до себе, тому при (p – 1)/2 ≤ deg(v1) справджуються такі нерівності:
У графі G довільна вершина, степінь якої не менший за (p – 1)/2, суміжна з кожною вершиною, степінь якої більший, ніж (p – 1)/2.
Якби нерівність p/2 ≤ deg(v) справджувалася при кожній вершині v графа G, то граф G був би повним, а тому гамільтоновим при 3 ≤ p. Це суперечить відсутності гамільтоних циклів у графі G. Отже граф G містить вершину v при deg(v) < p/2.
Виберемо за v1 вершину графа G з максимальним степенем m при m < p/2.
Згідно з вибором графа G як максимального негамільтонового графа, що задовольняє умови теореми, маємо:
кількість вершин, степінь яких не перевищує m, не перевищує m;
кількість вершин, степінь яких перевищує m (інакше кажучи, не менший від p/2), не менша від такої різниці:
Серед вершин, степінь яких не менший від p/2, виберемо вершину vp, несуміжну з v1.
Як вже зазначено у пунктах 2 і 3, існує гамільтонів ланцюг v1 v2 ... vp – 1 vp, причому вершина vp не суміжна з будь-якою вершиною vk, при якій vk + 1 суміжна з v1.
Справджуються нерівності: p/2 ≤ deg(vp) ≤ p – 1 – deg(v1) = p – 1 – m,
звідки маємо: m ≤ p/2 – 1 < (p – 1)/2.
Згідно з припущеннями щодо графа G, кількість вершин, степінь яких не перевищує m, менша за m. Тому серед вершин, суміжних з v1, знайдеться щонайменше одна вершина w, степінь якої не менший, ніж p/2. Таким чином, можна вказати пару несуміжних вершин w і vp, степені яких не менші, ніж p/2.
Отримана суперечність з пунктом 5 свідчить про хибність припущення щодо можливості існування негамільтонових графів з вказаними в умові теореми властивостями.
Зауваження 1. Умова доведеної теореми не є необхідною умовою гамільтоновості графа.
У графі G(V, E), усі ребра якого утворюють один цикл, що проходить через кожну вершину по одному разу, ця умова не справджується:
У графі, утвореному ребрами правильного 12-гранника (див. рис. 1), маємо:
Поша подав формулювання й доведення теореми — Lajos Pósa, Hamiltonian circuits in random graphs // Discrete Mathematics, 1976, 14(4), P.359–364 — після результів:
Дірака — Gabriel Andrew Dirac, Some theorems on abstract graphs // Proceedings of the London Mathematical Society, 1952, 2, P.69–81;
Оре — Øystein Ore, A Note on Hamiltonian Circuits // American Mathematical Monthly, 1960, 67, P.55,
сформульованих далі як наслідки відповідно 1 і 2. Через p, як і в теоремі 1, в них позначено кількість вершин графа G, через deg(v) — степінь вершини v, тобто кількість ребер графа G, кінцем яких є вершина v.
Наслідок 1. Якщо 3 < p і p/2 ≤ deg(v) при довільній вершині v графа G, то G — гамільтонів граф.
Наслідок 2. Якщо 3 ≤ p і p ≤ deg(v) + deg(w) при довільних несуміжних вершинах v і w графа G, то G — гамільтонів граф.
Означення 2. Запровадимо такі поняття.
Граф, який задовільняє умову Дірака (наслідка 1), називають графом Дірака.
Граф, який задовільняє умову Оре (наслідка 2), називають графом Оре.
Граф, який задовільняє умову Поши (теореми 1), називають графом Поши.
Зауваження 2.
Граф Оре є графом Дірака.
Граф Дірака є графом Поши.
Граф Поши не завжди є графом Дірака:
візьмемо повний граф з достатньо великою кількістю вершин;
долучимо до графа ще одну вершину й сполучимо її лише з двома вершинами початкового графа;
виберемо довільний гамільтонів цикл новоствореного графа;
вилучимо ребро, що не належить до вибраного гамільтонового циклу;
утворений граф буде задовольняти умову Поша;
утворений граф буде задовольняти умову Оре, бо матиме дві пари несуміжних вершин (долучена вершина та кінець вилученого ребра), сума степенів яких менша, ніж число вершин графа.
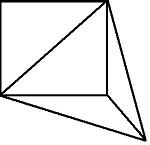
Граф Дірака не завжди є графом Оре — див. рис. 3, де подано приклад графа Оре, що має всього 5 вершин: 2 вершини степеня 4, 2 вершини степеня 3 і одну вершину степеня 2. Цей граф не є графом Дірака, бо 2 < 5/2.
Розглянемо рекурсивну функцію Hamilton, що набуває булевих значень, з такими параметрами цілого типу:
v — остання знайдена вершина;
w — вершина, з якої починають пошук;
d — довжина ланцюга, який ще потрібно пройти.
Якщо d = 1 і w суміжна з v, повертаємо величину «істина».
Позначаємо вершину v як «використана».
Серед вершин u, суміжних з v, шукаємо таку, яку ще не використано і для якої справджується Hamilton(u, w, d – 1).
Якщо вершина u з вказаними властивостями існує, то повертаємо величину «істина», записавши вершину u як чергову вершину гамільтонового циклу.
Позначаємо вершину v як «невикористана».
Повертаємо величину «хибність».
Алгоритм обчислення цієї функції має багато спільних рис з «пошуком у глибину» і передбачає оптимізований перебір з реалізацією однією групою операторів невідомої наперед кількості вкладених циклів. Альтернативою до рекурсивності є використання міток, що «більшістю голосів» вважають неприйнятним. Але це може виявитися прийнятним і виправданим для олімпіадної роботи.
Зауваження 3. Для знаходження гамільтонових шляхів, що не є циклами, достатньо у пункті 1 поданого алгоритму відмовитися від суміжності вершин w та v.
Зауваження 4. Рекурсивний пошук гамильтонового циклу може вимагати експоненціального (за кількістю вершин) часу.
Доведення. Розглянемо зв'язний граф, утворений сполученням одним ребром двох компонент — повних графів без спільних вершин —, що мають по 3 і p вершин, 3 ≪ p. Функція Hamilton не знайде гамільтонового циклу, але дослідить усі p! шляхів ребрами другої компоненти, що починаються у вибраній початковій вершині першої компоненти — кінця долученого ребра.
Подамо приклад програмної реалізації мовою Turbo Pascal.
{$I+}
const
nv_=10000; {Верхня межа кiлькостi вершин}
w: word =20; {Початокова вершина}
type pointv=^vertex;
vertex= record v: word; {Вершина}
n: pointv end;
aw= array[1..nv_] of word;
av= array[1..nv_] of pointv;
ab= array[1..nv_] of boolean;
var n0,n: ^av; {Сумiжнi вершини}
notused: ^ab; {Мiтки щодо використання}
num: ^aw;{Кiлькiсть сумiжних вершин}
o: text; {Вихiдний файл}
x: pointv;
nv, {Кiлькiсть вершин графа}
d, {Довжина ланцюга,
який ще потрiбно знайти}
j,k: word;
function hamilton(v: word): boolean;
var u: word; h: boolean;
BEGIN
if (d=1) then BEGIN
if num^[v] < num^[w] then begin
n^[v]:=n0^[v];
repeat h:= (w=n^[v]^.v);
n^[v]:=n^[v]^.n
until (n^[v]=nil) or h end
else begin
n^[w]:=n0^[w];
repeat h:= (v=n^[w]^.v);
n^[w]:=n^[w]^.n
until (n^[w]=nil) or h end;
if h then write(o,w,' ') END
else BEGIN
h:=false;
notused^[v]:=false;
n^[v]:=n0^[v];
dec(d);
repeat u:=n^[v]^.v;
if notused^[u]
then h:=hamilton(u);
n^[v]:=n^[v]^.n;
until (n^[v]=nil) or h;
inc(d);
notused^[v]:=not h;
if h and (d>1)
then write(o,u,' ') END;
hamilton:=h END;
{Врахування сумiжностi вершин k, j}
procedure edge(j,k: word); BEGIN
if nv < j then nv:=j;
inc(num^[j]);
new(x);
x^.v:=k;
x^.n:=nil;
if n0^[j]=nil then n0^[j]:=x
else n^[j]^.n:=x;
n^[j]:=x END;
BEGIN
assign(o,'HAMILTON.DAT');
reset(o); nv:=0;
new(n0); new(n); new(notused);
new(num);
for j:=1 to nv_ do begin
n^[j]:=nil;
n0^[j]:=nil;
num^[j]:=0 end;
{Зчитування пар вершин ребер}
repeat read(o,j,k);
edge(j,k);
edge(k,j);
until seekeof(o); close(o);
assign(o,'HAMILTON.RES');rewrite(o);
for j:=1 to nv do notused^[j]:=true;
d:=nv;
if hamilton(w) then writeln(o,w)
else writeln(o,'0');
close(o) END.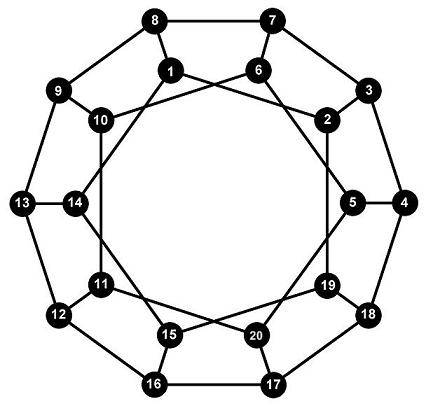
Вхідний файл HAMILTON.DAT, побудований згідно з рисунком 4, має такий вигляд.
1 2 1 8 1 14 2 3 2 19 3 4 3 7 4 5 4 18 5 6 5 20 6 7 6 10 7 8 8 9 9 10 9 13 10 11 11 12 11 20 12 13 12 16 13 14 14 15 15 16 15 19 16 17 17 18 17 20 18 19
Тоді вихідний файл матиме єдиний рядок з таким вмістом.
20 11 12 16 17 18 19 15 14 13 9 10 6 7 8 1 2 3 4 5 20
— отримано гамільтонів цикл вершинами 12-гранника, поданий рисунком 1.
Максимальна кількість послідовних викликів рекурсивної функції («глибина занурення») дорівнює кількості вершин, зменшеній на 1. Тому компілятори можуть накладати обмеження на кількість вершин обсягом оперативної пам'яті, відведеної для стеку. Наприклад, для простого циклу при максимальному для Turbo Pascal 7.0 об'ємі стеку 65520 байт переповнення відбувається при кількості вершин 5417, хоча для довільної меншої кількості вершин все гаразд. За рахунок використання міток можна позбутися рекурсивності, переписавши код функції hamilton, наприклад, таким чином.
function hamilton (w: word): boolean;
var v: ^aw; h: boolean;
label NEXTd,NEXTv,FIN; BEGIN
{Вставку початкiв
у списки iнцендентних ребер здiйснюємо
для зручностi подальшого програмування}
for j:=1 to nv do begin
new(x); x^.n:=n0^[j]; n0^[j]:=x end;
new(v); v^[d]:=w;
NEXTd: n^[v^[d]]:=n0^[v^[d]];
notused^[v^[d]]:=false;
NEXTv: if d=1 then BEGIN
if num^[v^[d]] < num^[w] then begin
repeat h:= (w=n^[v^[d]]^.v);
n^[v^[d]]:=n^[v^[d]]^.n
until (n^[v^[d]]=nil) or h end
else begin
n^[w]:=n0^[w];
repeat h:= (v^[d]=n^[w]^.v);
n^[w]:=n^[w]^.n
until (n^[w]=nil) or h end;
if h then goto FIN else begin
notused^[v^[d]]:=true;
inc(d); goto NEXTv end END
else BEGIN
repeat n^[v^[d]]:=n^[v^[d]]^.n;
if n^[v^[d]] =nil
then h:=true
else h:=notused^[n^[v^[d]]^.v]
until h;
if n^[v^[d]] <> nil then begin
v^[d-1]:=n^[v^[d]]^.v;
dec(d);
goto NEXTd end
else begin
notused^[v^[d]]:=true;
inc(d);
if d>nv then begin
h:=false; goto FIN end
else goto NEXTv end END;
FIN: if h then begin
write(o,w,' ');
for d:=1 to nv-1 do
write(o,v^[d],' ') end;
hamilton:=h END;
ЛітератураБерж К. Теория графов и ее применения. — М.: Издательство иностранной литературы, 1962.
Седжвик Р. Фундаментальные алгоритмы на C++. Алгоритмы на графах. — СПб: ООО «ДиаСофтЮП», 2002.
Харари Ф. Теория графов. — М.: Мир, 1973.