Задачі логічного характеру,
запропоновані 5-класникам
(Математична газета — 2014. — № 07–08 — С. 17–27)
Передмова
Публікація містить збірку 51 завдань переважно логічного характеру з повним і стислим розв'язанням. Цю збірку пропонували як завдання на літо учням, зарахованим у 5 (математичний) клас Києво-Печерського ліцею № 171 «Лідер» у червні 2013 року. Автор зіткнувся з цією збіркою як батько учениці, яка розв'язувала ці завдання. Власне з розв'язанням більшості задач проблем не було. Але були проблеми зі стислим описом розв'язання.
З одного боку, понятійний апарат умов та розв'язання цих завдань доступний учням 4 класу. З іншого боку, компетенції щодо фахового мовлення, символьного запису й унаочнення (див. Загальний підхід до формування переліку компетенцій щодо опанування природничо-математичними дисциплінами // Математика у сучасній школі, 2012, № 1, с. 29–32) лише починають формуватися після закінчення початкової школи. І особливо при розв'язуванні задач логічного характеру. Якщо навіть учень 5 класу самостійно отримає відповідь до такої задачі, він навряд чи зможе самостійно й коректно описати її розв'язання.
Запровадження пропедевтичного курсу логіки у початковій школі, наприклад, з другого класу, ніяк вирішує і не полегшує вирішення проблеми мовлення, символьного запису й унаочнення. Зазвичай у робочих зошитах відведеного на розв'язання місця достатньо лише для написання відповіді й натяків на розв'язання. Це стає особливо очевидним, якщо врахувати розмір літер почерку школяра початкової школи. Інакше кажучи, автори посібників не вважають за потрібне навчати учнів початкової школи так, щоб не було потреби їх переучувати. Проблему неможливо вирішити, запровадивши окремі зошити для запису повноцінного розв'язання. Швидкість писання учнів початкової школи така, що записування триватиме істотно довше від часу, протягом якого учень спроможний концентрувати увагу. Щоб не відбити бажання дітей займатися такими завданнями й математикою взагалі, вчителі зазвичай не звертають увагу на довершеність розв'язання таких задач у початковій школі.
Якщо ще можна і треба сподіватися від учнів самостійно породити ідеї розв'язання, то самостійно опанувати загальноприйнятими прийомами висловлення думки для них буде не під силу. Навіть у старших клаcах. Колись таки потрібно починати знайомити учнів з прийомами стислого запису розв'язання і вимагати від них аналогічного оформлення. Як уже сказано, до 5 класу — рано. Після 8 класу — пізно, бо цьому завадить потужний потік понятійного апарату багатьох предметів. У тому числі й математики. На думку автора публікації, починати найкраще у 6 класі, а результати такої виснажливої (і для учня, і для вчителя) роботи проявляться не раніше, ніж за три роки.
Підготовка у педагогічних вишах і у минулому, й зараз не передбачає вироблення стійких навичок розв'язування і навчання розв'язування логічних задач. Тому допомагати потрібно і учням, і студентам, і вчителям. Хоча б поданням таких розв'язань, що все зрозуміло і жодного слова викинути неможливо. Особливу увагу потрібно приділяти тим завданням, які при першому знайомстві непосильні для учнів суто з психологічних міркувань. У поданій збірці це такі:
№ 2 — відповідь залежить від тлумачення умови, що не є однозначною;
№ 16 — багатоваріантність відповіді та свідоме уникнення унаочнення з метою стислішого викладу;
№ 17 — багатоваріантність відповіді та уважне ставлення до умови (у якій не сказано, що на батьківські збори прийшли батьки всіх учнів;
№ 29 — вимагається довести хибне твердження, тому потрібно подати контриприклади;
№ 44 — множина розв'язків незліченна та існують значення параметрів задачі, при яких істотно змінюється поведінка досліджуваної системи, що не є очевидним з умови задачі.
Готувати потрібно й до таких завдань. Учень повинен бути готовим до будь-яких несподіванок на контрольних, ЗНО чи олімпіадах (запланованих чи пропущених упорядником завдання), а результат його роботи не має залежати від наявності таких несподіванок.
Публікацію адресовано вчителям математики загально освітніх навчальних закладів і студентам математичних спеціальностей педагогічних університетів.
Мета публікації: познайомити з прикладами максимально стислого оформлення розв'язання задач логічного характеру невисокої складності.
Завдання 1. Чи можливо квадрат 5 × 5 клітин разрізати на дві однакові частини таким чином, щоб лінія розрізу йшла сторонами клітин? Відповідь обґрунтуйте.
Розв'язання.
При такому розрізанні кожна клітина повністю потрапляє лише до однієї з фіґур. У кожній з фіґур буде натуральна кількість клітин. Якщо фіґури однакові, то кількість клітин у них однакова. У цьому випадку загальна кількість клітин квадрату мала би бути парною. Але 25 — непарне число, тому розрізати описаним способом квадрат на дві різні фіґури неможливо.
Відповідь: неможливо.
Завдання 2. Розділіть квадрат 4 × 4 на чотири однакові частини таким чином, щоб лінії розрізу йшли сторонами клітин. Скільки різних способів розрізаня Ви знайдете?
Відповідь:
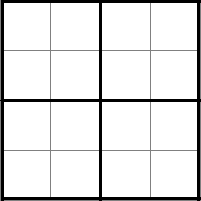
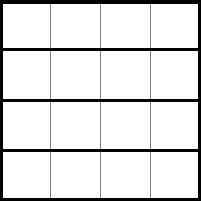
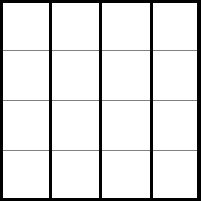












Кількість способів розрізання: 6 з точністю до рухів фіґури, 15, якщо сторони нерухомі.
Завдання 3. На столі лежать 5 червоних і 5 синіх паличок різної довжини. Суми довжин паличок одного кольору однакові. Чи можливо розпиляти ці палички таким чином, щоб їх потім можна було розташувати парами паличок однакової довжини й різного кольору?
Розв'язання. Викладемо палички одного кольору вздовж прямої лінії. Викладемо палички іншого кольору вздовж паралельної лінії таким чином, щоб початки й кінці послідовностей паличок дотикалися. Рухаючи пилку від початку послідовності поличок до їх кінця, зустрівши стик паличок одного кольору, розрізаємо паличку іншого кольору. Отримаємо потрібне розташування парами. Отже розрізати можна.
Відповідь: можливо.
Завдання 4. В кімнаті стоять табуретки і стільці. У кожної табуретки — 3 ніжки, у кожного стільця — 4 ніжки. Якщо на всіх стільцях і табуретках сидять люди, в кімнаті 39 ніг. Скільки в кімнаті табуреток і скільки стільців?
Розв'язання. Якщо на табуретці сидить людина, то маємо всього 5 ніг, а якщо на стільці, то 6. Складемо таблицю, у якій через x позначимо кількість стільців.
| x | 6x | 39 – 6x | ⋮5 |
| 0 | 0 | 39 | ні |
| 1 | 6 | 33 | ні |
| 2 | 12 | 27 | ні |
| 3 | 18 | 21 | ні |
| 4 | 24 | 15 | так |
| 5 | 30 | 9 | ні |
| 6 | 36 | 3 | ні |
| 7 | 42 | – 3 | ні |
Відповідь: 4 стільці і 3 табуретки.
Завдання 5. Три приятелі Петро, Анатолій і Віталій підійшли до стоянки автомашин і мотоциклів. Милуючись машинами, Петро від нудьги підрахував усе транспортні засоби. Їх виявилося 45. Анатолій підрахував колеса — їх виявилося 115. Віталій зауважив, що мотоциклів з коляскою було удвічі менше, ніж мотоциклів без коляски. Скільки автомашин було на стоянці?
Розв'язання. Позначимо через x кількість мотоциклів з коляскою. Тоді:
3x — кількість коліс на мотоциклах з коляскою;
2x — кількість мотоциклів без коляски;
4x — кількість коліс на мотоциклах без коляски;
7x — кількість коліс на всіх мотоциклах.
Для різних величин x обчислимо (115 – 7x) — кількість коліс, які залишаються для машин. Ця кількість має бути кратна 4.
| x | 6x | 115 – 7x | ⋮4 |
| 0 | 0 | 115 | ні |
| 1 | 7 | 108 | так |
| 2 | 14 | 101 | ні |
| 3 | 21 | 94 | ні |
| 4 | 28 | 87 | ні |
| 5 | 35 | 80 | так |
| 6 | 42 | 73 | ні |
| 7 | 49 | 66 | ні |
| 8 | 56 | 59 | ні |
| 9 | 63 | 52 | так |
| 10 | 70 | 45 | ні |
| 11 | 77 | 38 | ні |
| 12 | 84 | 31 | ні |
| 13 | 91 | 24 | так |
| 14 | 98 | 14 | ні |
| 15 | 105 | 10 | ні |
| 16 | 112 | 3 | ні |
| 17 | 119 | – 4 | ні |
При x > 16 маємо: 115 – x > 0. Можливі величини x такі: 1, 5, 9, 13. Перевіримо, при якому з них кількість усіх транспортних засобів дорівнює 45.
| x | 3x + (115 – 7x) : 4 | = 45 |
| 1 | 3 · 1 + 108 : 4 = 3 + 27 = 30 | ні |
| 5 | 3 · 5 + 80 : 4 = 15 + 20 = 35 | ні |
| 9 | 3 · 9 + 52 : 4 = 27 + 13 = 40 | ні |
| 13 | 3 · 13 + 24 : 4 = 39 + 6 = 45 | так |
Відповідь: 6 автомашин.
Завдання 6. Ставши у круг, розмовляють 4 дівчинки: Ася, Валя, Галя й Ніна. Дівчинка в зеленій сукні (не Ася і не Валя) стоїть між дівчинкою у фіолетовій сукні і Ніною. Дівчинка у білій сукні стоїть між дівчинкою у рожевій сукні і Валею. Якого кольору сукню одягнула кожна з дівчаток?
Розв'язання. Складемо прямокутну таблицю, в якій першими літерами імен назвемо рядки, а першими літерами кольорів назвемо стовпчики. В цій таблиці позначимо плюсами або мінусами без індексів безпосередні наслідки простих речень умови («+», якщо дівчина має сукню певного кольору, інакше «–»). Заповнимо цю таблицю виходячи з того, що в кожному рядку і в кожному стовпчику має бути один і лише один плюс.
Індексом праворуч знизу вкажемо номер логічного кроку.
| з | ф | б | р |
|---|
| А | – | –2 | | |
|---|
| В | – | +2 | – | – |
|---|
| Г | +1 | –1 | –1 | –1 |
|---|
| Н | – | – | | |
|---|
Зобразимо схему розташування (з точністю до точки погляду: згори чи знизу).
Якщо Ніна матиме білу сукню, то вона має стояти між дівчиною в рожевій сукні і Валею. Але поряд з нею — Галя в зеленій сукні. Ці умови не сумісні. Отже, Надя має рожеву сукню, а Ася — білу. Схема розташування набуває такого вигляду,
що повністю узгоджено з умовою.
Відповідь: Аcя — у білій сукні, Ніна — в рожевій сукні, Галя — в зеленій сукні, Валя — у фіолетовій сукні.
Завдання 7. У школі працює 18 учителів. Кожний з них або добрий, або злий. Відомо, що серед будь-яких трьох учителів хоча б один добрий. Яке найбільше можливе число злих учителів?
Розв'язання.
Якщо злих вчителів немає, то серед будь-яких трьох вчителів всі добрі — умова справджується.
Якщо злий вчитель один,то серед будь-яких трьох вчителів 0 або 1 злий вчитель — умова справджується.
Якщо злих вчителів 2, то серед будь-яких трьох вчителів 0, 1 або 2 злих вчителя — умова справджується.
Якщо злих вчителів 3 або більше, то серед будь-яких трьох вчителів 0, 1, 2, 3 або більше — умова не справджується.
Відповідь: 2.
Завдання 8. Дід удвічі сильніший за Бабу, Баба утричі сильніша за Внучку, Внучка у 4 рази сильніша за Жучку, Жучка у 5 разів сильніша за Кішку, Кішка в 6 разів сильніша за Мишку. Без Мишки всі решта Ріпку витягнути не можуть, а з нею – можуть. Скільки потрібно Мишок, щоб вони самі витягнули Ріпку?
Розв'язання.
6 · 5 · 4 · 3 · 2 + 6 · 5 · 4 · 3 + 6 · 5 · 4 + 6 · 5 + 6 + 1 =
6 · 5 · 4 · 3 · (2 + 1) + 6 · 5 · 4 + 6 · 5 + 6 + 1 =
6 · 5 · 4 · (9 + 1) + 6 · 5 + 6 + 1 =
6 · 5 · 41 + 6 + 1 = 30 · 41 + 7 = 1230 + 7 = 1237.
Відповідь: 1237 Мишок.
Завдання 9. Довжина сходів між сусідніми поверхами дорівнює 10 м. Скільки метрів потрібно пройти, щоб піднятися з першого поверху на сьомий?
Розв'язання. Потрібно подолати (7 – 1) = 6 відстаней між поверхами, що складає 6 · 10 м = 60 м.
Відповідь: 60 метрів.
Завдання 10. В запису ***5 : 11 = ** замініть зірочки цифрами таким чином, щоб отримати рівність, що справджується.
Розв'язання. Умову задачі можна записати так ***5 = ** ⋅ 11. Запис у «стовпчик» має такий вигляд:
**
× 11
----
**
+ **
----
***5
Аналізуючи розряд одиниць маємо: запис двоцифрового числа — співмножника 11 — закінчується цифрою 5. При додаванні двох чисел у «стовпчик» у наступний розряд переносять не більше ніж 1. Для того, щоб добуток був чотирицифровим числом необхідно, щоб запис двоцифрового числа — співмножника 11 — починався цифрою 9. Маємо:
95
× 11
----
95
+ 95
----
1045
Відповідь: 1045 : 11 = 95.
Завдання 11. Василь задумав ціле число. Микола помножив його чи то на 5, чи то на 6. Євген додав до результату Миколи чи то 5, чи то 6. Сашко відняв від результату Євгена чи то 5, чи то 6. У результаті вийшло 73. Яке число задумав Василь?.
Розв'язання. В результаті виконання двох останніх дій число зростає на одне з таких чисел:
+ 5 – 5 = 0;
+ 5 – 6 = –1;
+ 6 – 6 = 0;
+ 6 – 5 = 1
Після виконання першої дії отримали одне з таких чисел: 72, 73 або 74 за умови, що воно кратне 6 або 5. Отже, це число 72. А задумане число у 6 разів менше – 72 : 6 = 12.
Відповідь: 12.
Завдання 12. Для фарбування поверхні куба потрібно 6 г фарби. Після висихання фарби куб розпиляли на 8 однакових кубиків. Скільки потрібно фарби, щоб розфарбувати не зафарбовані частини їхньої поверхні?
Розв'язання. В кубі 6 однакових граней. На кожну грань витратили 6 : 6 = 1 (грам фарби). Якщо куб розділити на 8 однакових кубиків, то кожне ребро потрібно поділити навпіл. Всього потрібно здійснити 3 розрізання. У кожному перерізі — квадрат, однаковий за розмірами з гранню. Але для кожного розрізу новостворені кубики потрібно фарбувати по обидва боки від розрізу. Отже, пофарбувати потрібно поверхню, площа якої така сама, як у 6 граней. На це потрібно витратити 6 грамів фарби.
Відповідь: 6 грамів.
Завдання 13. В Андрія і Бориса разом 11 горіхів, у Андрія і Володимира — 12 горіхів, у Бориса й Володимира — 13 горіхів. Скільки всього горіхів у Андрія, Бориса й Володимира разом?
Розв'язання. Позначимо першими літерами імен хлопців кількості горіхів у них. Маємо:
А + Б = 11;
А + В = 12;
Б + В = 13.
Кожну літеру записано у двох рівняннях. Додавши праві та ліві частини всіх трьох рівнянь, отримаємо:
2А + 2Б + 2В = 36.
Поділивши обидві частини останнього рівняння на 2, отримаємо: А + Б + В = 18.
Відповідь: 18 горіхів.
Завдання 14. Вздовж бігової доріжки розставлено 19 прапорців на однаковій відстані один від одного. Михайло стартує від першого прапорця й біжить зі сталою швидкістю. Через 7 секунд він опиняється біля 7-го прапорця. За який час Михайло добіжить до 19-го прапорця?
Розв'язання. Від першого до 19 прапорця розташовано (19 – 1) = 18 проміжків. Від 1-го до 7-го розташовано (7 – 1) = 6 проміжків. Михайло всю відстань подолає за час, що у 18 : 6 = 3 рази перевищує 7 секунд, тобто за 21 секунду.
Відповідь: Михайло добіжить від першого до 19-го прапорця за 21 секунду.
Завдання 15. На дошці записано 3 двоцифрових числа, запис одного з яких починається на 5, іншого — на 6, а третього — на 7. Учитель попросив трьох учнів вибрати довільні два з цих трьох чисел і додав їх. Перший учень отримав 147, результати другого і третього – різні 3-цифрові числа, запис яких починається з 12. Які числа записано на дошці?
Розв'язання. Зауважимо: 5 + 6 = 11, 5 + 7 = 12, 7 + 6 = 13. При додаванні двох чисел у наступний розряд переносять не більше ніж 1 одиницю. Нехай записані числа мають вигляд: 5А, 6В, 7С (у цьому розв'язанні такі записи будемо тлумачити як записи двоцифрових чисел, а не як запис добутків). Маємо:
-
6В + 7С = 147,
60 + В + 70 + С = 147,
В + С = 147 – 130 = 17 = 9 + 8,
{В, С} = {8, 9};
-
5А + 6В = 12Х = 120 + Х,
110 + А + В = 120 + Х,
А + В = 120 + Х – 110 = 10 + Х ≥ 10,
А ≥ 10 – В;
-
5А + 7С = 12Y,
50 + 70 + А + С = 120 + Y,
120 + А + С = 120 + Y,
А + С = 120 + Y – 120 = Y < 10,
А < 10 – С.
Маємо: 10 – В ≤ А < 10 – С при В = 8 і С = 9 або В = 9 і С = 8.
2 = 10 – 8 ≤ А < 10 – 9 = 1 – таке неможливе.
1 = 10 – 9 ≤ А < 10 – 8 = 2 – таке справджується при А = 1.
Відповідь: 51, 69, 78.
Завдання 16. Відстань між двома авто на шосе дорівнює 100 км. Швидкості машин складають 80 км/год і 60 км/год. Яка буде відстань між ними (вздовж шосе) за годину?
Розв'язання.
Запровадимо на шосе систему координат таким чином, щоб у початковий момент одна з машин мала координату 0 і швидкість v0, інша — координату 100 (км) і швидкість v1, де:
-
або v0 = ± 60 км/год і v1 = ± 80 км/год;
-
або v0 = ± 80 км/год і v1 = ± 60 км/год.
Зауважимо: незалежний вибір обох знаків в обох випадках ніяк не обмежено умовою. Через проміжок часу t (у годинах) координати машин будуть такі (в кілометрах):
x0 = v0t;
x1 = v1t + 100,
а відстань між машинами складе:
|x1 – x0| = | v1t + 100 – v0t | =
| (v1 – v0)t + 100 |.
Підставивши в останню формулу час t = 1 і всі допустимі варіанти поєднання v0 і v1, отримаємо:
| (80 + 60) · 1 + 100 | = 240;
| (80 – 60) · 1 + 100 | = 120;
| (– 80 + 60) · 1 + 100 | = 80;
| (– 80 – 60) · 1 + 100 | = 40;
| (60 + 80) · 1 + 100 | = 240;
| (60 – 80) · 1 + 100 | = 80;
| (– 60 + 80) · 1 + 100 | = 120;
| (– 60 – 80) · 1 + 100 | = 40.
Відповідь: можливі такі варіанти: 40 км, 80 км, 120 км або 240 км.
Завдання 17. У класі 30 учнів класу. Їхні батьки пришли на збори. Мам було 24, тат — 18. У скількох учнів на збори прийшли одночасно й тато, й мама?
Розв'язання. Позначимо через:
М — кількість учнів, у яких прийшла мама;
Т — кількість учнів, у яких прийшов тато;
МТ — кількість учнів, у яких прийшли мама і тато одночасно;
Y — кількість учнів, у яких прийшов хоча б хтось із батьків, У ≤ 30.
Маємо:
(М – МТ) — кількість учнів, у яких прийшла лише мама;
(Т – МТ) — кількість учнів, у яких прийшов лише тато;
Y = (М – МТ) + МТ + (Т – МТ) = М + Т – МТ,
звідки МТ = М + Т – Y ≥ 24 + 18 – 30 = 12.
З іншого боку:
МТ ≤ М = 24;
МТ ≤ Т = 18.
Остаточно маємо: 12 ≤ МТ ≤ 18.
Відповідь: одне з таких чисел: 12, 13, 14, 15, 16, 17, 18.
Завдання 18. В рюкзаку лежить 4 банки: дві з вершками і дві з молоком. Навмання виймають 2 банки. Якщо вони з однаковим вмістом, то їх використовують на сніданок, а в рюкзак кладуть банку з молоком. Якщо банки з різним вмістом, то їх також використовують на сніданок, а в рюкзак кладуть банку з Вершками. В решті решт у рюкзаку залишилася одна банка. Що в ній: молоко чи вершки?
Розв'язання. Зобразимо на схемі всі можливі варіанти маніпуляцій: В — банка з вершками, М — з молоком.
2В+2М
↙ ↘
3M 2В+1M
↓ ↙ ↓
2M 2В
↓ ↙
1M
Відповідь: банка з молоком.
Завдання 19. Яке число має стояти замість знаку * у послідовності: 7, 17, 37, 77, * , …, 317, …?
Розв'язання. Для даної послідовності остання цифра дорівнює 7, а результат її відкидання з степенем двійки, зменшеним на 1. Також можна сказати, що результат відкидання 7 для наступного члена є подвоєним результатом відкидання для поточного члена, збільшеним на 1: 0, 1, 3, 7, 15, 31, 63…
Відповідь: 157.
Завдання 20. У магазин привезли 223 л масла у бідонах по 10 і 17 л. Скольки було бідонів?
Розв'язання. Позначимо через А кількість бідонів по 10 л, через В — кількість бідонів по 17 л. Маємо:
223 = 10А + 17В ⇔ 10А = 223 – 17В.
Переберемо усі можливі величини В.
| B | 223 – 17B | ⋮10 |
|---|
| 0 | 223 | ні |
| 1 | 206 | ні |
| 2 | 189 | ні |
| 3 | 172 | ні |
| 4 | 155 | ні |
| 5 | 138 | ні |
| 6 | 121 | ні |
| 7 | 104 | ні |
| 8 | 87 | ні |
| 9 | 70 | так |
| 10 | 53 | ні |
| 11 | 36 | ні |
| 12 | 19 | ні |
| 13 | 2 | ні |
| 14 | – 15 | ні |
Маємо: А = 7, B = 9, A + B = 16.
Відповідь: 16 бідонів.
Завдання 21. На лісовій галявині зібралися друзі: Папуга, Удав, Слоненя, Теля, Кошеня, Мавпочка і Верблюженя. Папуга почав усіх вимірювати. Виявилося, що Слоненя довше від Теляти на 3 папуги, Верблюденя довше Мавпочки також на 3 папуги, Теля довше від Папуги на 7 папуг, Верблюденя довше Кошеняти на 6 папуг, а сумарна довжина всіх дорівнює довжині Удава, довжина якого складає 38 папуг. Знайдіть довжини друзів у папугах.
Розв'язання. Позначимо першими літерами імен персонажів їх довжини. Маємо:
(1) С = Т + 3П;
(2) В = М + 3П;
(3) Т = 8П;
(4) В = К + 6П;
(5) У = 38П;
(6) У = П + С + Т + К + М + В.
Виразимо змінні через П:
(7) С = 11П — див.(1,3)
(8) М = К + 3П — див. (2,4)
(9) М + К + В = У – П – С – Т = 18П — див. (6, 5, 7, 3)
(10) В = М + 3П = К + 6П — див. (2, 8)
(11) К + М + В = 3К + 9П — див.( 10, 8)
(12) К = (18П – 9П) : 3 = 3П — див. (11, 9)
(13) М = К + 3П = 6П — див. (12, 8)
(14) В = К + 5П = 9П — див. (12, 4)
Відповідь: У = 38П, С = 11П, Т = 8П, К = 3П, М = 6П, В = 9П.
Завдання 22 Микола й Вітя, гуляючи парком, вийшли велику круглу галявину, обсажену липами. Микола пішов навкруги поляни, рахуючи дерева. Вітя зробив те саме, але розпочав з іншого дерева. Дерево, яке у Миколи було 20-м, у Віті було 7-м, а 7-е — 94-м. Скільки дерев росло навкруги галявини?
Розв'язання. Розглянемо нумерацію дерев у випадку, коли хлопці рухалися у протилежних напрямках (нижній рядок таблиці заповнено справа наліво).
| Микола | … | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | … |
|---|
| Вітя | …
| 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | … |
|---|
20 ≠ 94. Отже, хлопці рухались в одному напрямку, а дерева нумерували таким чином (нижній рядок таблиці заповнено з обох сторін):
| Микола | … | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | … |
|---|
| Вітя | …
| 94 | 95 | 96 | 97 | 98 | 99 | 100 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
|---|
Відповідь: 100 дерев.
Завдання 23. Порвано книгу. З книги випав шмат. Перша сторінка куска має номер 387, а номер останньої складається з тих самих цифр, але записаних у іншому порядку. Скільки сторінок випало з книги?
Розв'язання. Номер останньої сторінки має бути більшим за 387 і парним. Отже, цей номер 738. Випало 738 – 387 + 1 = 352 сторінки або 352 : 2 = 176 аркушів
Відповідь: 352 сторінок.
Завдання 24. Учитель задав на уроці мудрувату задачу. Кількість хлопців, що розв'язали цю задачу, збігається з кількістю дівчат, що її не розв'язали. Кого у класі більше: тих, хто розв'язав задачу, чи дівчат?
Розв'язання. Запровадимо такі величини:
Х+ — кількість хлопчиків, які розв'язали задачу;
Х– — кількість хлопчиків, які не розв'язали задачу;
Д+ — дівчата, які розв'язали задачу;
Д– — дівчата, які не розв'язали задачу.
Маємо:
Х+ = Д– — згідно з умовою задачі;
Х+ + Д+ — кількість тих, хто розв'язав задачу;
Д– + Д+ — кількість дівчат.
Останні дві величини збігаються, бо Х+ = Д–.
Відповідь: кількості однакові.
Завдання 25. Десятеро людей прийшли в гості у калошах. Йшли назад вони по одному, й кожний взував довільну пару калош, у яку він міг влізти (тобто не меншого розміру, ніж його власний). Яка найбільша кількість людей, що не змогли взути калоші?
Розв'язання. Занумеруємо людей натуральними числами від 1 до 10 у порядку зростання розміру їхнього взуття. Розглянемо такий порядок і спосіб взування, при якому після кожного кроку максимально зменшується вибір: 1-ий взує калоші 10-го, 2-ий — 9-го, 3-й — 8-го, 4-й — 7-го, 5-й — 6-го. При цьому без калош залишиться 5 людей.
Відповідь: 5.
Завдання 26. Прилетіли галки, сіли на палки. Якщо на кожній палці сяде по галці, то для однієї галки не хватит палки. Якщо на кожній палці сяде по дві галки, то одна з палок буде без галок. Скільки було палок і скільки було галок?
Розв'язання. Позначимо через Г кількість галок, через П — кількість палок. Маємо:
Г = П + 1 = 2(П – 1) = 2П – 2, звідки П = 3, Г = 4.
Відповідь: 3 палки і 4 галки.
Завдання 27. Чотири близнюки — Петро, Микола, Борис і Василь — святкували свій день народження. Їм подарували коробку цукерок. Домовившись розділити цукерки порівну, хлопці пішли грати з гостями. Микола зайшов до кімнати першим, взяв свою частину й пішов. Через деякий час до кімнати зайшов Петро, взяв четверту частину цукерок і пішов. Те саме зробили Борис і Василь, після чого у коробці залишилася 81 цукерка. Скільки всього у коробці було цукерок і скільки цукерок взяв кожний з близнюків? Хто і скільки цукерок має взяти ще?
Розв'язання. Позначимо через x початкову кількість цукерок. Після дії кожного хлопця залишилося 3/4 кількості цукерок. Маємо:
x · (3/4) · (3/4) · (3/4) · (3/4) = 81,
x · (3 · 3 · 3 · 3)/(4 · 4 · 4 · 4) = 81,
x · 81/256 = 81,
x / 256 = 1,
x = 256.
Відповідь: x / 4 = 64 — кількість цукерок, які повинен був взяти кожен з братів;
Микола взяв 256 / 4 = 64 (цукерки), йому не треба нічого брати;
Петро взяв 256 – 64 / 4 = 192 / 4 = 48 (цукерок), йому треба взяти 64 – 48 = 16 (цукерок);
Бориc взяв 192 – 48 / 4 = 144 / 4 = 36 (цукерок), йому треба взяти 64 – 36 = 28 (цукерок);
Вася взяв 144 – 36 / 4 = 108 / 4 = 27 (цукерок), йому треба взяти 64 – 27 = 37 (цукерок).
Завдання 28. У трьох ящиках насипано крупу, вермішель і цукор. На першому ящику написано «крупа», на другому — «вермішель», на третьому — «крупа або цукор». Що у який ящик насипано, якщо вміст кожного ящика не відповідає надпису на ньому?
Розв'язання. Складемо прямокутну таблицю, в якій назвемо рядки номерами ящиків, а стовпчики — (можливим) вмістом. У цій таблиці позначимо плюсами або мінусами без індексів безпосередні наслідки простих речень умови: «+», якщо в ящику це є, інакше — «–». Заповнимо цю таблицю, виходячи з того, що в кожному рядочку і в кожному стовпчику має бути один і лише один плюс, а решта — мінуси. Індексом праворуч вкажемо номер логічного кроку.
Відповідь: у ящику 1 — цукор, у ящику 2 — крупа, у ящику 3 — вермішель.
Завдання 29. На дошці написано 1*2*3*4*5*6*7*8 = 20. Замість символу «*» на дошці у невідомому порядку можна написати символи «+» або «–». Доведіть, що рівність не може справджуватися.
Відповідь:
1 – 2 + 3 + 4 + 5 – 6 + 7 + 8 =
1 + 2 – 3 + 4 – 5 + 6 + 7 + 8 =
1 + 2 + 3 + 4 + 5 + 6 + 7 – 8 = 20
— довести неможливо, бо є 3 контрприклади. Якщо 20 замінити на довільне непарне число, то доведення можна побудувати на міркуванні, що ліва частина рівності завжди парна.
Завдання 30. У таблиці 4×4 розставити 7 зірочок таким чином, щоб при викреслюванні довільних двох рядків і довільних двох стовпчиків у решті клітин була хоча б одна зірочка.
Розв'язання. Потрібно отримати таке розташування зірочок, щоб після викреслення двох стовпчиків зірочки були у трьох різних рядках:
Відповідь: див. розташування, подане вище. Інші можна отримати за допомогою перестановок рядків і стовпчиків.
Завдання 31. 16 слив розклали на столі так, як показано на рисунку нижче.
* * * *
* * * *
* * * *
* * * *
Потім 6 слив з'їли, при цьому у кожному рядку й у кожному стовпчику залишилися парні кількості слив. Нарисуйте, як лежать ті сливи, що залишилися.
Розв'язання. З кожного рядочка і з кожного стовпчика взяти парну кількість слив. Існує рядок з якого не брали жодної сливи, бо інакше забрали б не менше 8-ми слив. Аналогічно, існує стовпчик, з якого не брали жодної сливи. З чотирьох рядків 4-ма способами можна вибрати 1 рядок, заповнений сливами. З чотирьох стовпчиків 4-ма способами можна вибрати 1 стовпчик заповнений сливами. У вибраних рядку і стовпчику буде розташовано 7 слив. Залишаться 3 рядки і 3 стовпчики, які міститимуть по 1-й сливі. Вільних слив залишиться 3. Кожну з них потрібно розташувати в 1-му з трьох стовпчиків. Це можна зробити такою кількістю способів: 3 · 2 · 1 = 6. Отже, кількість всіх способів дорівнює: 4 · 4 · 6 = 96.
Відповідь: існує 96 таких розташувань. Наприклад, такі.
· · * *
· * · *
* · · *
* * * *
· · * *
· * · *
* * * *
* · · *
Завдання 32. На шахову дошку пролили фарбу. Чи може кількість заляпаних клітин бути на 17 менше від кількості чистих клітин?
Розв'язання. Доведемо неможливість від супротивного. Припустимо, що таке можливо. Позначимо через x кількість заляпаних клітин, тоді кількість незаляпаних клітин дорівнює x + 17, а загальна кількість — 2x + 17 = 64. Ліворуч — непарне число, а праворуч — парне. Отримана суперечність свідчить про хибність суперечність.
Відповідь: неможливо.
Завдання 33. Чи можливо відміряти 8 літрів води, перебуваючи біля струмка з двома відрами ємністю 15 літрів і 16 літрів?
Розв'язання. Подамо таблицею дані про наповнення відер після наповнень відра ємністю 16 літрів і наступних переливань.
| 15 | 0 | 15 | 0 | 1 | 1 | 15 | 0 | 2 | 2 | 15 | 0 | 3 | 3 | 15 | 0 | 4 | 4 | 15 | 0 | 5 | 5 | 15 | 0 | 6 | 6 | 15 | 0 | 7 | 7 | 15 |
|---|
| 16 | 16 | 1 | 1 | 0 | 16 | 2 | 2 | 0 | 16 | 3 | 3 | 0 | 16 | 4 | 4 | 0 | 16 | 5 | 5 | 0 | 16 | 6 | 6 | 0 | 16 | 7 | 7 | 0 | 16 | 8 |
|---|
Відповідь: можливо, наприклад згідно з поданою вище схемою переливань.
Завдання 34. Розставте числа 1, 1, 2, 2, 3, 3, 4, 4 у такому порядку, щоб між одиницями була одна цифра, між двійками — дві, між трійками — три, а між четвірками — чотири цифри.
Відповідь: 41312432 або 23421314.
Завдання 35. Два хлопчики катались на човні. До берега підійшов загін солдат. Човен такий малий, що ним можуть переправитися двоє хлопців або лише один солдат. Чи можуть солдати переправитися через річку?
Розв'язання. Опишемо процес переправи одного солдата.
Хлопці, човен і солдат — на березі, з якого переправляється.
Хлопці — на різних берегах, солдат і човен — на березі з якого переправляється.
Хлопці на різних берегах річки, солдат і човен — на березі, на який переправляється.
Хлопці і човен — на березі з якого здійснено переправу, солдат — на іншому березі.
Таким чином солдатів можна переправити один за одним.
Відповідь: переправа можлива.
Завдання 36. На кільцевій дорозі проводять естафету мотоциклістів. Лінії старту й фінішу естафети збігаються. Мотоциклісти рухаються колом в одному напрямку. Довжина кола 350 км. Довжина кожного етапу 75 км. Яка найменша кількість етапів може бути в цій естафеті?
Розв'язання. Шукана кількість x задовольняє умову: 75 x кратне 350.
1 спосіб: 75 = 3 · 52, 350 = 2 · 52 · 7, звідки x = 2 · 7 = 14.
2 спосіб:
| x | 75x | ⋮350 |
| 1 | 75 | ні |
| 2 | 150 | ні |
| 3 | 225 | ні |
| 4 | 300 | ні |
| 5 | 375 | ні |
| 6 | 450 | ні |
| 7 | 525 | ні |
| 9 | 675 | ні |
| 10 | 750 | ні |
| 11 | 825 | ні |
| 12 | 900 | ні |
| 13 | 975 | ні |
| 14 | 1050 | так |
Відповідь: 14 етапів, які складуть 3 повних кола.
Завдання 37. Розділіть дану фігуру на 9 однакових фігур.
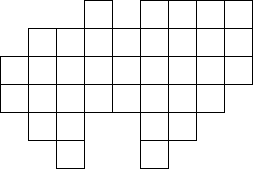
Відповідь:

Завдання 38. Машина їде зі сталою швидкістю 60 км/год. На скільки потрібно збільшити її швидкість, щоб виграти по одній хвилині на кожному пройденому кілометрі?
Розв'язання. Машина проїздить 1 км за 1 хв. Якщо вона виграватиме 1 хв на 1 км, то має долати цей кілометр миттєво, що неможливо з фізичної точки зору. Якщо б її швидкість була меншою (наприклад, при швидкості 30 км/год машина проїздить 1 км за 2 хв), то це було б можливо (приріст швидкості складе 30 км/год для такої самої початкової швидкості).
Відповідь: це неможливо.
Завдання 39. Ганна, Борис, Віра й Гена спіймали разом 10 рибин і всі різну кількість. Ганна спіймала більше за всіх, а Віра менше за всіх. Хто спіймав більше рибин: хлопчики чи дівчатка?
Розв'язання. 1 + 2 + 3 + 4 = 10, тому діти виловили такі кількості рибин: 1, 2, 3, 4. Дівчата виловили 1 + 4 = 5 (рибин), а хлопці — 2 + 3 = 5 (рибин).
Відповідь: кількості однакові.
Завдання 40. Яку цифру у рівності 9А : 1А = А замінено літерою А? Тут у лівій частині рівності записано відношення двох двоцифрових чисел.
Розв'язання. Розглянемо, чи справджуються рівність для кожного значення відмінної від 0 цифри.
| А | 1А | 1А · А |
| 1 | 11 | 11 |
| 2 | 12 | 24 |
| 3 | 13 | 39 |
| 4 | 14 | 56 |
| 5 | 15 | 75 |
| 6 | 16 | 96 |
| 7 | 17 | 119 |
| 8 | 18 | 144 |
| 9 | 19 | 171 |
Відповідь: А = 6.
Завдання 41. Кожним ударом силач Бамбула розбиває шмат граніту на 4 частини. На скільки шматків він розколов гранітну брилу, якщо зробив 666 ударів?
Розв'язання. При кожному ударі кількість шматків збільшується на 3. Шукана кількість дорівнює 1 + 666 · 3 = 1999.
Відповідь: 1999 шматків.
Завдання 42. У магічному квадраті сума чисел у кожному рядку, стовпчику і на діагоналі одна й та сама. Знайдіть число N, якщо відома лише частина чисел цього магічного квадрата.
Розв'язання. 10 + 9 + 14 = 33 — сума в усіх рядках, стовпчиках і на діагоналі. Заповнимо квадрат, вказавши для кожного числа індексом праворуч знизу номер логічного кроку.
Відповідь: N = 17.
Завдання 43. По колу розташовано 9 шестерень так, що перша шестерня зчеплена з другою, друга — з третьою і т.д., а дев'ята — з першою. Чи можуть ці шестерні обертатися?
Розв'язання. Розглянемо випадок, коли остання шестерня не сполучена з першою. Будемо обертати першу шестерню у напрямку руху годинникової стрілки. Дві зчеплені шестерні обертаються у протилежних напрямках. Шестерні з непарним номером будуть обертатися за рухом годинникової стрілки. Шестерні з парними номерами будуть обертатися проти напрямку руху годинникової стрілки. Після зчеплення першої шестерні з дев'ятою рух стане неможливим.
Відповідь: шестерні не можуть обертатися.
Завдання 44. З пунктів А і В одночасно назустріч один одному вийшли два хлопчики, кожний зі своєю, але сталою швидкістю, і зустрілися за годину. Після цього вони, не зупиняючись, пішли далі й, дійшовши до пунктів В і А, повернули назад. Скільки часу пройде між їхніми першою та другою зустрічами?
Розв'язання. Розглянемо випадок, коли хлопці зустрілися вдруге після того, як кожен з них змінив напрям руху. Відстань між пунктами хлопці проходять разом за одну годину. Між зустрічами їм потрібно пройти подвоєну відстань між пунктами за 2 години.
Якщо відношення більшої швидкості до меншої швидкості дорівнює 2, тоді вперше вони зустрінуться у точці, що поділяє відрізок АВ у відношенні 1 : 2 (чи 2 : 1), а вдруге — у пункті B (чи А). І саме через 2 години.

AC : BC = 1 : 2 =(AC + AB) : BC
Якщо відношення швидкостей хлопців перевищує 2, хлопці зустрінуться вдруге після того, як лише один з них змінив напрям руху, а інший ні. Чим більше відношення швидкостей, тим менша відстань між точками зустрічі і час на їх подолання.
Відповідь: не більше 2 годин.
Завдання 45. Сума дев'яти різних натуральних чисел дорівнює 46. Які це числа?
Розв'язання. Сума дев'яти найменших різних натуральних чисел дорівнює:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. Щоб отримати відповідь, потрібно до одного з цих чисел додати одиницю без порушення умови, що всі числа різні.
Відповідь: 1, 2, 3, 4, 5, 6, 7, 8, 10.
Завдання 46. Якщо чотиризначне число N поділити на 2 чи на 9, то у кожному випадку отримають тризначне число, записане трьомя однаковими цифрами. Знайдіть число N.
Розв'язання. Згідно з умовою задачі існують такі цифри x та у, при яких:
N = 2 · x · 111 = 9 · у · 111, звідки 2 · x = 9 · у. Права та ліва частини останньої рівності кратні 9. Тому x = 9, у = 2, N = 2 · 999 = 1998.
Відповідь: N = 1998.
Завдання 47. Дорогу довжиною 28 км поділили на три нерівні частини. Відстань між серединами крайніх частин дорівнює 16 км. Знайдіть довжину середньої частини.
Розв'язання. Позначимо через А, В, С довжини ділянок, А + В + С = 28 (км).

Маємо:
А/2 + В/2 + В/2 + С/2 = 16;
(А + В + С + В) : 2 = 16;
28 + В = 16 · 2 = 32;
В = 32 – 28 = 4.
Відповідь: 4 кілометри.
Завдання 48. Олекса задумав число. Він додав до нього 5, потім розділив суму на 3, помножив на 4, відняв 6, розділив на 7 і отримав число 2. Яке число задумав Олекса?
Розв'язання. Виконаємо обернені дії у зворотному порядку з кінцевим результатом:
(2 · 7 + 6) : 4 · 3 – 5 = (14 + 6) : 4 · 3 – 5 = 20 : 4 · 3 – 5 = 5 · 3 – 5 = 15 – 5 = 10.
Відповідь: 10.
Завдання 50. Білий ведмідь вийшов на прогулянку з Північного полюсу. Він пройшов 10 км на південь, потім — 10 км на схід, а потім — 10 км на північ. На якій відстані від Північного полюсу він опинився?
Розв'язання. Рух на схід чи на захід є рухом вздовж паралелі й не змінює відстані до полюсів.
Відповідь: 0 кілометрів.
Завдання 51. Вздовж огорожі ростуть 8 кущів малини. Число ягід на сусідніх кущах відрізняється на 1. Чи може на всіх кущах разом бути 2013 ягід?
Розв'язання. Якщо числа відрізняються на 1, то вони різної парності. З 8-ми чисел — кількостей ягід на кущах малини — 4 парних і 4 непарних. Сума таких чисел парна і не може дорівнювати 2013.
Відповідь: загальна кількість ягід відмінна від 2013.
Завдання 51. Домовик Нафаня купив зошит об'ємом 96 аркушів і занумерував всі її сторінки по порядку від 1 до 192. Домовик Кузя вирвав з цього зошита 25 аркушів і додав усі 50 чисел, які на них написано. Чи могло у нього вийти число 2012?
Розв'язання. З 50 послідовних натуральних чисел 25 парних і 25 непарних. Сума таких чисел непарна і тому відмінна від 2012.
Відповідь: сума номерів сторінок відмінна від 2012.


















