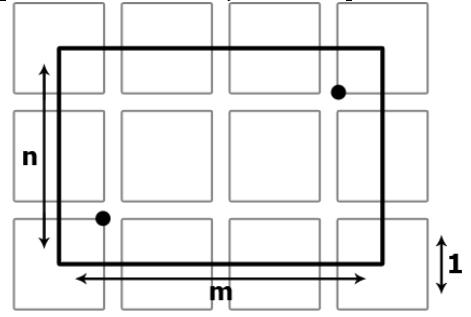
Рис. 1. Схема міста Ідеальне. Межі міста позначено грубою чорною лінією.
1. Шахи
Максимальна оцінка: 100 балів
Обмеження на час: 3 сек.
Обмеження на пам'ять: 32 MБ
Вхідний файл: chess.in
Вихідний файл: chess.out
Програма: chess.*
Петрик зацікавився шахами. Проте традиційні шахи йому наскучили досить швидко — одразу після того, як він зайняв перше місце з шахів серед юніорів. Тепер він цікавиться варіаціями на тему шахових фігур на різноманітних дошках. Наразі, Петрика цікавіть кількість варіантів розташування довільної (можливо, нульової) кількості шахових коней на дошці 4×N так, щоб вони не атакували один одного. Проте він не любить працювати з великими числами, і тому Петрику достатньо знайти остачу від ділення цієї кількості на деяке число P. Допоможіть йому у цьому нелегкому завданні.
Завдання
Обчислити остачу від ділення на P кількості можливих розміщень шахових коней на дошці 4×N, при яких вони не атакують один одного.
Вхідні дані
В єдиному рядку вхідного файлу записано два натуральних числа — довжина дошки N (2 ≤ N ≤ 109) і дільник P (2 ≤ P ≤ 109).
Вихідні дані
Єдиний рядок вихідного файлу має містити одне ціле число — остачу від ділення на P кількості можливих розміщень шахових коней на дошці 4 на N, при яких вони не атакують один одного.
Примітка
Шаховий кінь (на рисунку позначено літерою К) атакує до 8 клітин (на цьому самому рисунку позначено літерою А).
| A | A | |||
| A | A | |||
| K | ||||
| A | A | |||
| A | A |
Для 15% тестів N ≤ 7.
Для 70% тестів N ≤ 10000.
Приклади
| chess.in | chess.out |
|---|---|
| 2 7 | 4 |
| 3 6 | 2 |
| 5 5 | 4 |
2. Школа
Максимальна оцінка: 100 балів
Обмеження на час: 0,5 сек.
Обмеження на пам’ять: 32 MБ
Вхідний файл: school.in
Вихідний файл: school.out
Програма: school.*
Петро П’яточкін учиться в школі. Торік він їздив до школи тролейбусами, але після подорожчання проїзних квитків збагнув, що швидше і зручніше діставатись туди пішки. Місто Ідеальне, де мешкає Петрик,— це прямокутник завбільшки m на n кварталів, складений з однакових квадратних блоків. Межа міста проходить не вздовж межі кварталів, а ділить їх навпіл або «відрізає» від кутових кварталів чвертинки — див. схему міста на рис 1.

Петрик вирушає до школи з найпівденнішого та водночас найзахіднішого з кутів кварталів, що належать місту, та прямує до найпівнічнішого та найсхіднішого кута, де розташовано вхід до школи. Початковий та кінцевий пункти позначено на рис. 1 міста жирними крапками. Хлопець може пересуватися лише межами кварталів (самі квартали, ясна річ, забудовано) та переходити з вершини одного кварталу на вершину сусіднього лише перпендикулярно до напряму вулиці — паралельно межам міста. Для кожного перехрестя визначено тривалість t горизонтального (зі сходу на захід і навпаки) та вертикального (з півночі на південь і назад) руху. Кожний світлофор працює так: протягом перших t секунд світлофор дозволяє горизонтальний рух і забороняє вертикальний, протягом наступних t дозволяє вертикальний (та забороняє горизонтальний), з 2(t + 1)-ої секунди до 3t-ої знову дозволяє горизонтальний і т. д. Для різних перехресть ця величина t може бути різною. Пройти один бік кварталу Петрик може за хвилину. Вулицю хлопець переходить за секунду — коли світлофори це дозволяють. Переходити ж на червоне світло та виходити за межі міста Петрик не хоче — це надто небезпечно.
Завдання
Допоможіть Петрикові визначити, за який найкоротший проміжок часу він може дійти до школи. Відомо, що в момент, коли Петрик виходить з дому, всі світлофори саме дозволяють горизонтальний рух.
Вхідні дані
У першому рядку вхідного файла вказано натуральні числа m та n — ширину й висоту міста. Ці числа не перевищують 250.
Подальший уміст файла — n рядків. При i та j таких, що
1 ≤ i ≤ n,
1 ≤ j ≤ m, j-те число (i + 1)-го рядка — тривалість руху на відповідному перехресті. Це число натуральне й не перевищує 500. В кожному рядку перераховано перехрестя від найзахіднішого до найсхіднішого, в першому рядку описано найпівнічніші перехрестя, в останньому — найпівденніші.
Вихідні дані
Вихідний файл повинен містити єдине число — тривалість найменшого проміжку часу (в секундах), якого Петрикові достатньо, щоб дістатись до школи.
Приклад
| school.in | school.out |
|---|---|
|
3 2 1 2 3 3 5 6 | 187 |
Пояснення до прикладу
Петрик може дістатись до школи за 187 секунд: він вийде з дому й одразу перейде дорогу в горизонтальному напрямі; зачекає 2 секунди, поки світлофор дозволить рух у вертикальному напрямі, й перейде дорогу на північ; дістанеться протилежного кута кварталу за 120 секунд і, оскільки відповідний світлофор дозволятиме горизонтальний рух, одразу ж перейде вулицю та продовжуватиме рух у східному напрямі, поки не дійде до наступного перехрестя. Він встигне перейти вулицю у вертикальному напрямі в останню секунду, коли світлофор дозволяє це робити, і зараз же востаннє перейде дорогу, та дістанеться до школи. Шлях Петрика позначено на схемі. Число в куті кварталу на схемі позначає кількість секунд, яку Петрику необхідно витратити, щоб дістатись до цього кута.
Легко побачити, що швидше ніж за 187 секунд хлопець до школи не потрапить. Справді, якби Петрику взагалі не доводилось чекати на зелене світло, він міг би дістатись до школи щонайшвидше за 185 секунд (він мав би тричі пройти вздовж кварталів та п’ять разів перейти вулицю). З іншого боку, перед тим як уперше перейти вулицю в північному напрямі — хай скільки кварталів він пройде в східному — хлопцю потрібно чекати щонайменше 2 секунди.
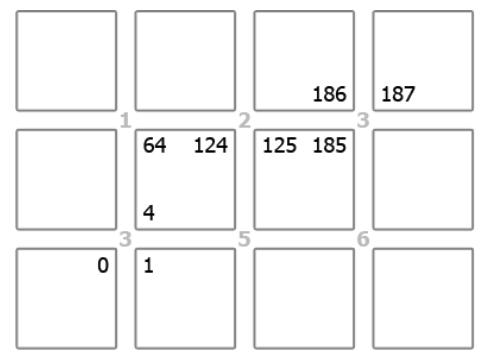
Рис. 2. Один з оптимальних шляхів Петрика до школи
для поданого прикладу вхідних даних.