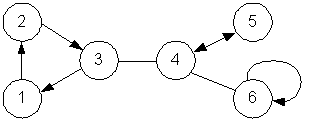
Рис 1. Один з можливих планів патрулювання
для поданого далі прикладу вхідних даних.
1. Музей
Максимальна оцінка: 100 балів
Обмеження за часом: 0,75 сек.
Обмеження за пам’яттю: 32 MБ
Вхідний файл: museum.in
Вихідний файл: museum.out
Програма: museum.*
У столиці країни Олімпія збудований Музей Олімпійської Слави, де виставлено нагороди школярів країни з різних предметних олімпіад. Будівля музею складається з виставкових зал, з’єднаних коридорами. Коридор сполучає саме дві зали. Відомо, що кожної зали музею можна дістатися з будь-якої іншої зали, прямуючи коридорами. Також відомо, що кількість коридорів дорівнює кількості залів.
Уночі музей патрулюють охоронці. Кількість охоронців дорівнює кількості зал, та у кожен момент часу охоронець доглядає за своєю залою. Кожну годину згідно плану патрулювання деякі з охоронців переходять в іншої зали, а інші залишаються на місті. План патрулювання відповідає таким вимогам:
Для кожної зали план задає чи залишиться її охоронець на місці, чи перейде до певної зали, яка сполучена з даною коридором.
Після переходів охоронців, у кожній залі повинен опинитися саме один охоронець.
Щогодини застосовують один і той самий план патрулювання.

Згідно планом, поданим на рис. 1, щогодини:
а охоронець зали 6 усю ніч проводить у цій залі.
Завдання
Знайдіть остачу від ділення на P кількості різних планів патрулювання музею.
Вхідні дані
Перший рядок вхідного файлу містить пару цілих чисел N (3 ≤ N ≤ 50 000) – кількість залів у музеї, та P (2 ≤ P ≤ 10 000).
Наступні N рядків містять пари цілих чисел від 1 до N – номери залів, що з’єднано коридором.
Вихідні дані
Єдиний рядок вихідного файлу має містити ціле число – кількість планів патрулювання музею за модулем P, тобто остачу від ділення цієї кількості на P.
Примітка
Щонайменше у 20% тестів N ≤ 20.
Щонайменше у 60% тестів N ≤ 1000.
Приклад
| museum.in | museum.out |
|---|---|
|
6 1000 1 2 2 3 3 1 3 4 4 5 4 6 | 20 |
Пояснення до прикладу
Для поданого прикладу вхідних даних існує 20 різних планів патрулювання, що можна подати підстановками на 6-елементній множині:
(123456), (123546), (123654), (124356), (132456), (132546), (132654), (213456), (213546), (213654), (214356), (231456), (231546), (231654), (312456), (312546), (312654), (321456), (321546), (321654). Тут у дужках на j-ому місці подано образ j при відповідній підстановці. На рис. 1 зображено план (231546).
2. Пари точок
Максимальна оцінка: 100 балів
Обмеження за часом: 0,5 сек.
Обмеження за пам’яттю: 32 MБ
Вхідний файл: pairs.in
Вихідний файл: pairs.out
Програма: pairs.*
На площині своїми координатами задано N червоних та N синіх точок. Жодні три точки не належать до однієї прямої.
Завдання
Потрібно побудувати N відрізків таких, що жодні два з них не перетинаються, кожен відрізок з’єднує точки різного кольору, і кожна точка належить саме одному відрізку як його кінець.
Вхідні дані
Перший рядок вхідного файлу містить єдине натуральне число – кількість блоків тестових даних, що задано у файлі. Блоки слідують один за одним. Кожен блок необхідно опрацювати окремо.
Перший рядок кожного тестового блоку містить ціле число N (1 ≤ N ≤ 2500) – кількість точок одного кольору. Далі слідують набори координат синіх точок, а потім – червоних. Набір координат точок одного кольору задається N рядками, кожен з яких містить пару цілих чисел – x і y координати точки (| x | ≤ 10 000, | y | ≤ 10 000).
Вихідні дані
Вихідний файл має містити відповіді для всіх блоків тестових даних із вхідного файлу без розділення. Кожен з N рядків відповіді кожного з блоків має містити пару цілих чисел від 1 до N – номери синьої та червоної точок, сполучених відрізком. Точки пронумеровано у тому порядку, в якому подано їхні координати у вхідному файлі окремо для кожного кольору.
У випадку, якщо неможливо сполучити точки відрізками без перетинів, єдиний рядок відповіді для блоку має містити число 0.
Примітка
Щонайменше у 20% тестів буде справджуватися нерівність: N ≤ 10 та кількість блоків не перевищуватиме 2.
Приклад
| pairs.in | pairs.out |
|---|---|
|
2 2 1 1 3 5 4 10 2 2 1 1 1 2 2 |
1 2 2 1 1 1 |